SUCTF2019 - hardCpp

参考文献：去OLLVM平坦化([SUCTF2019]hardCPP) - Pinguw’s Blog

查壳，ELF64，无壳

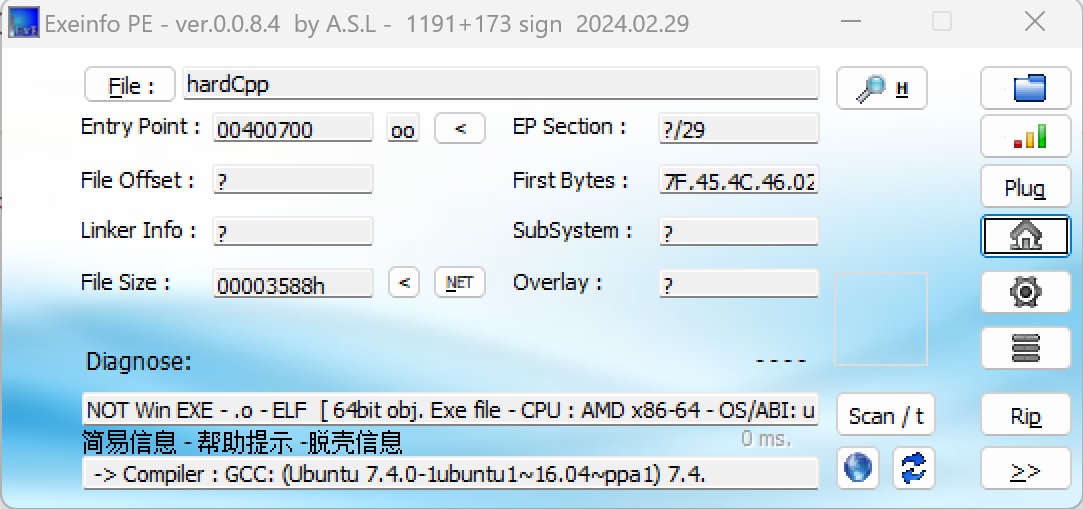
IDA中发现有多层while嵌套，内部有一个switch控制分发，观察程序流程图发现明显的平坦化痕迹。

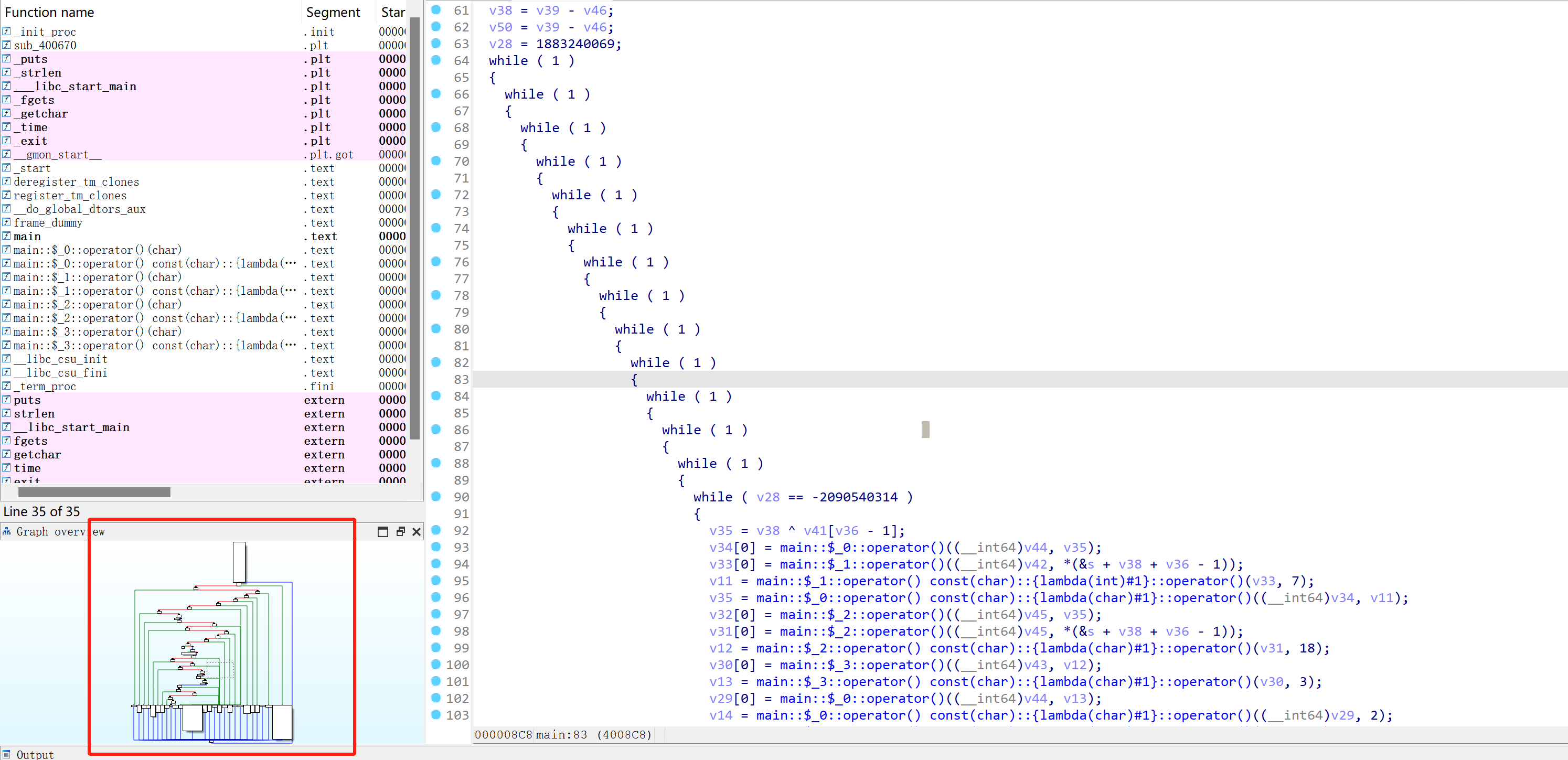
于是先采用脚本去平坦化。

安装angr。

pip install angr

下载deflat脚本https://github.com/Pure-T/deflat。

运行

python deflat.py hardCpp 0x4007E0   
#python + deflat.py + 文件名 + 起始地址(基本就是main函数的地址)

运行结果，去平坦化成功。（过程中Warning没有关系）

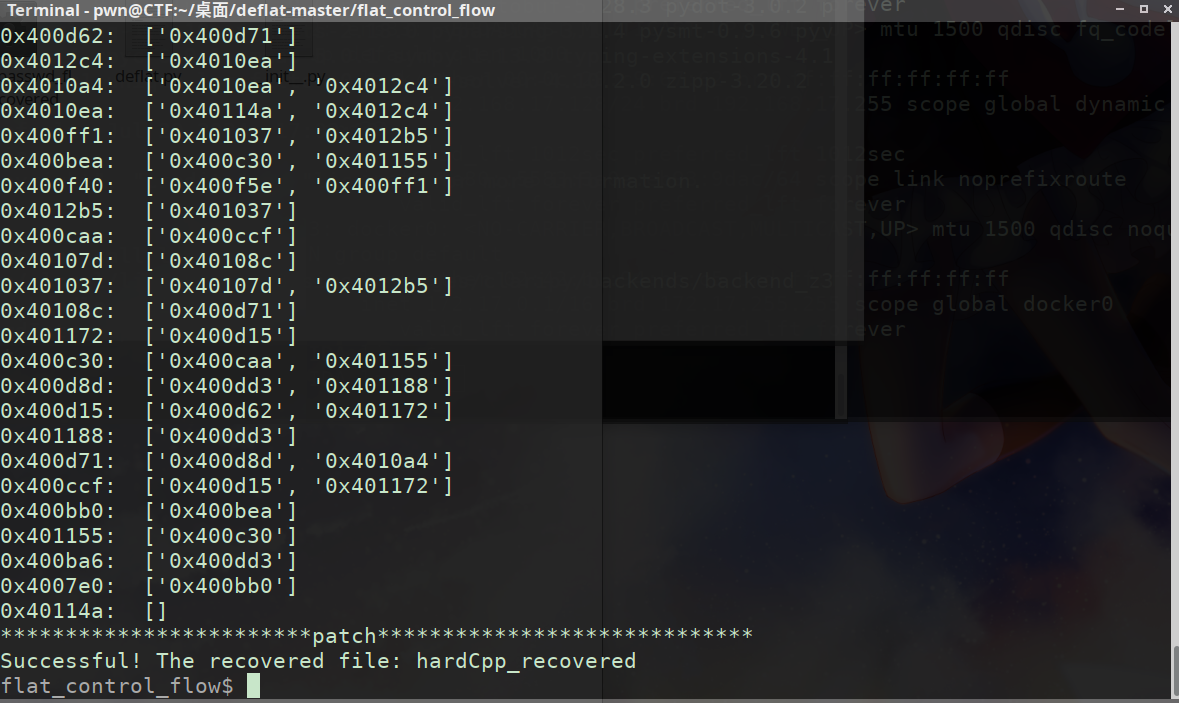
将hardCpp_recovered拖进IDA分析，

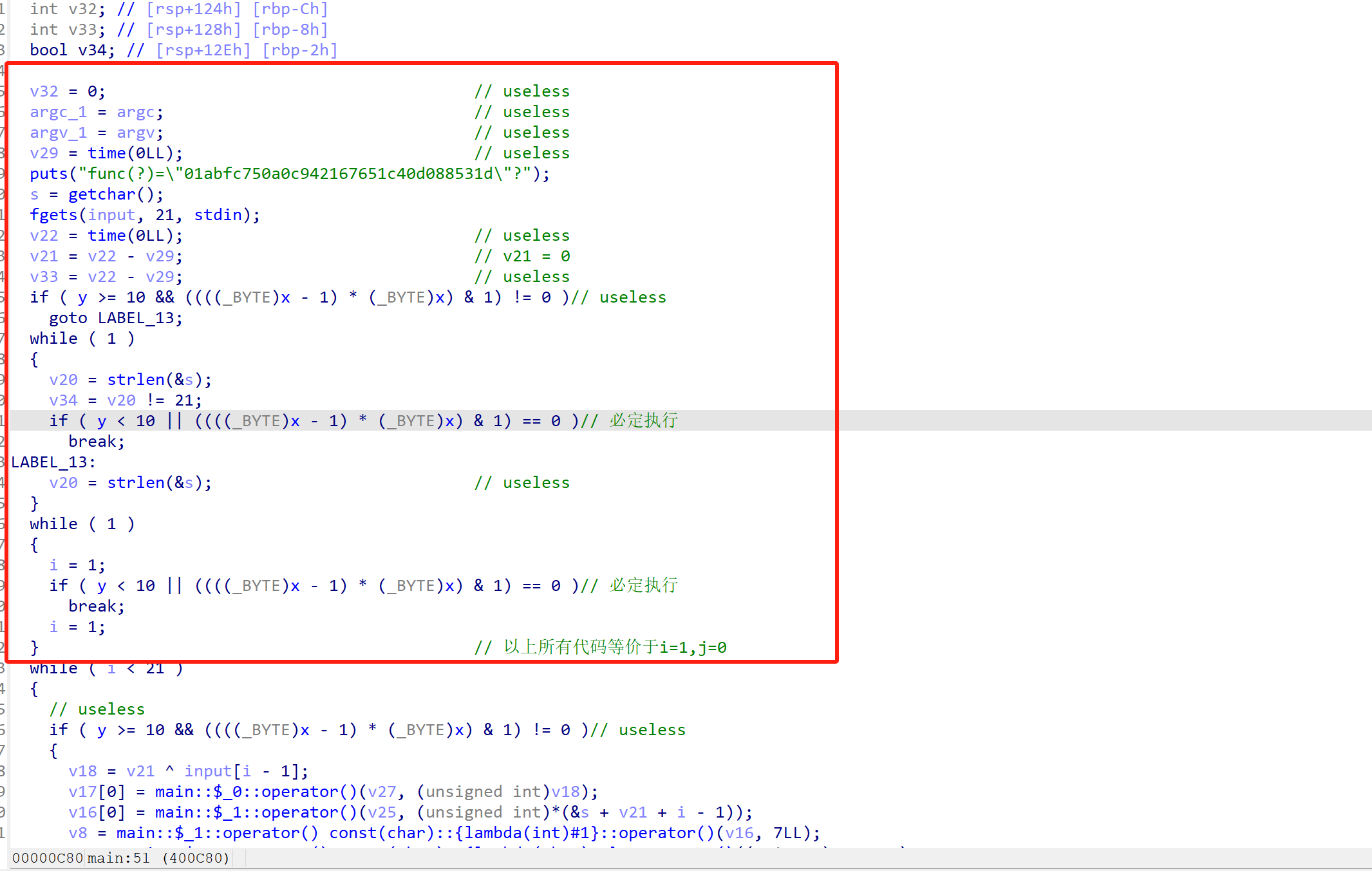
首先判断main开头的一段程序基本都是无效代码，将输入字符串重命名为input，后文有用到的两个变量重命名为i，j。另外在读入字符串前先读入了一个字符 s ，这个s的地址其实是input-1,是真实输入的字符串的开头，我们重命名为input_0。

这里要特别注意去平坦化后大量出现的((x - 1) * x) & 1的语句，因为相邻两个正整数的乘积为偶数，所以这样的语句结果恒为0。

然后进入循环，程序中形如main::$_1::operator() const(char)::{lambda(int)#1}::operator()(v16, 7LL)的大量函数，是c++11中的lambda表达式，

参考：深入浅出 C++ Lambda表达式：语法、特点和应用_c++ lambda函数作为函数参数 - CSDN博客

其实就是一种匿名函数，可以和正常函数一样分析。

在子函数中，依然存在未去平坦化的代码，因此我们将deflat起始地址设在每个子函数中再做一遍deflat。

python deflat.py hardCpp_recovered 0x401310
python deflat.py hardCpp_recovered_recovered 0x4016C0
python deflat.py hardCpp_recovered_recovered_recovered 0x4014E0

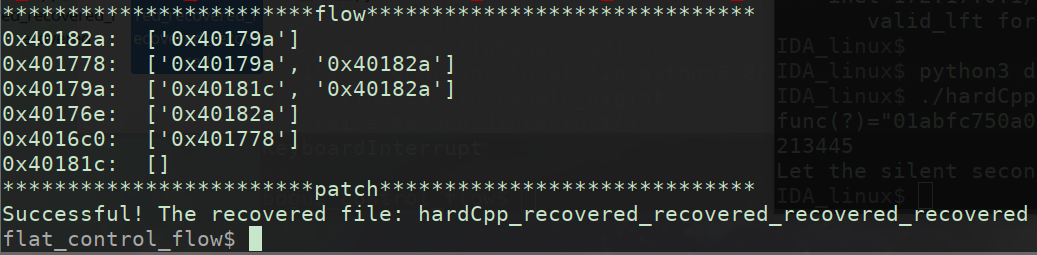
去平坦化后，我们分析子函数，以main::$_0::operator() const(char)::{lambda(char)#1}::operator()()为例子

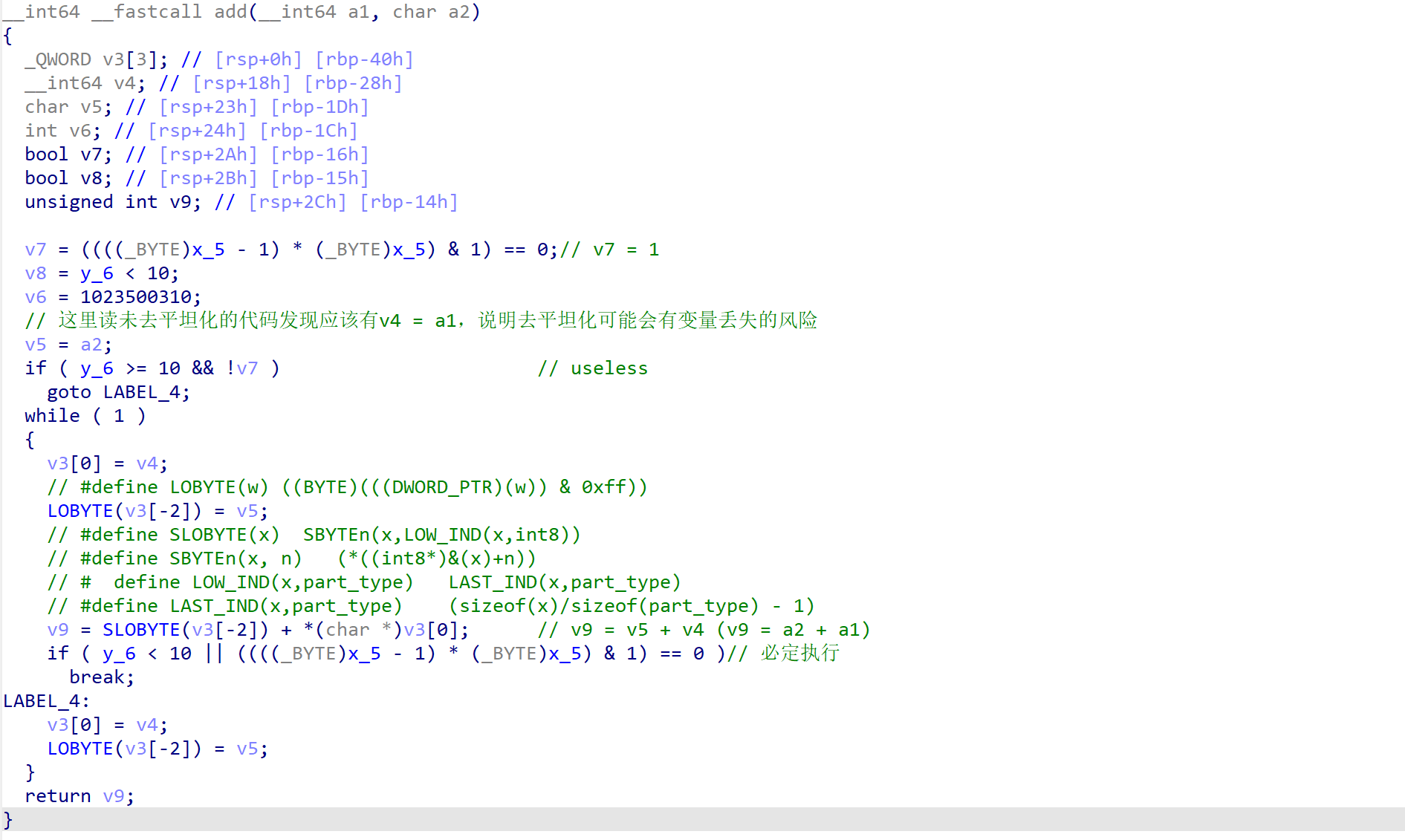
去掉混淆后，函数作用其实就是返回两数的和（int_8下），将函数重命名为add。

同理，我们将每个子函数以此方法分析功能并重命名。

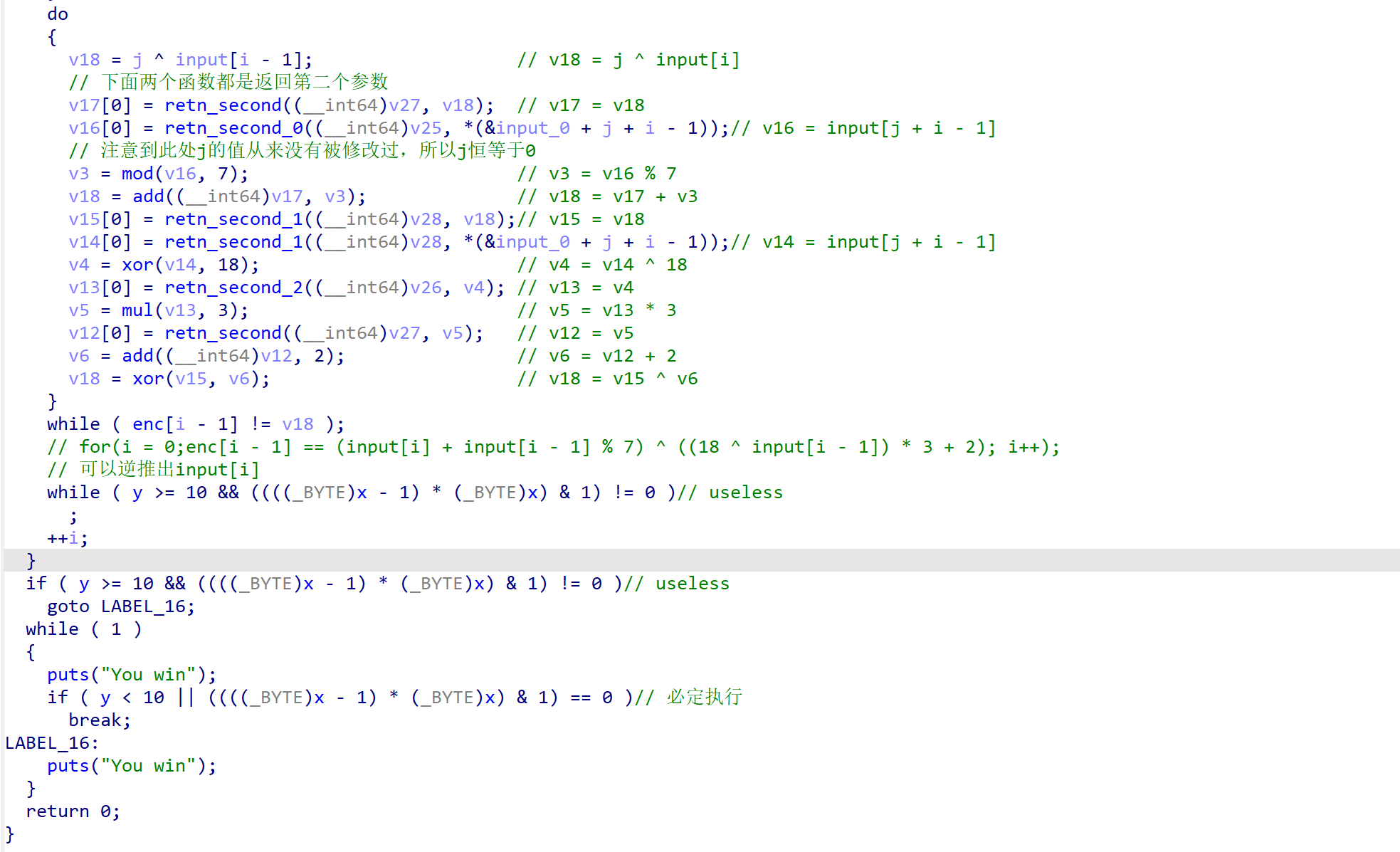
得出结论是循环中执行的语句是v18 = (input[i] + input[i - 1] % 7) ^ ((18 ^ input[i - 1]) * 3 + 2)，虽然fail的代码部分在去平坦化过程丢失了，但是还是可以看出要想跳出循环，必须满足对于$i<21$，有enc[i - 1] = (input[i] + input[i - 1] % 7) ^ ((18 ^ input[i - 1]) * 3 + 2)

这个式子是可逆的，即已知enc[i - 1]和input[i - 1]可以求input[i]

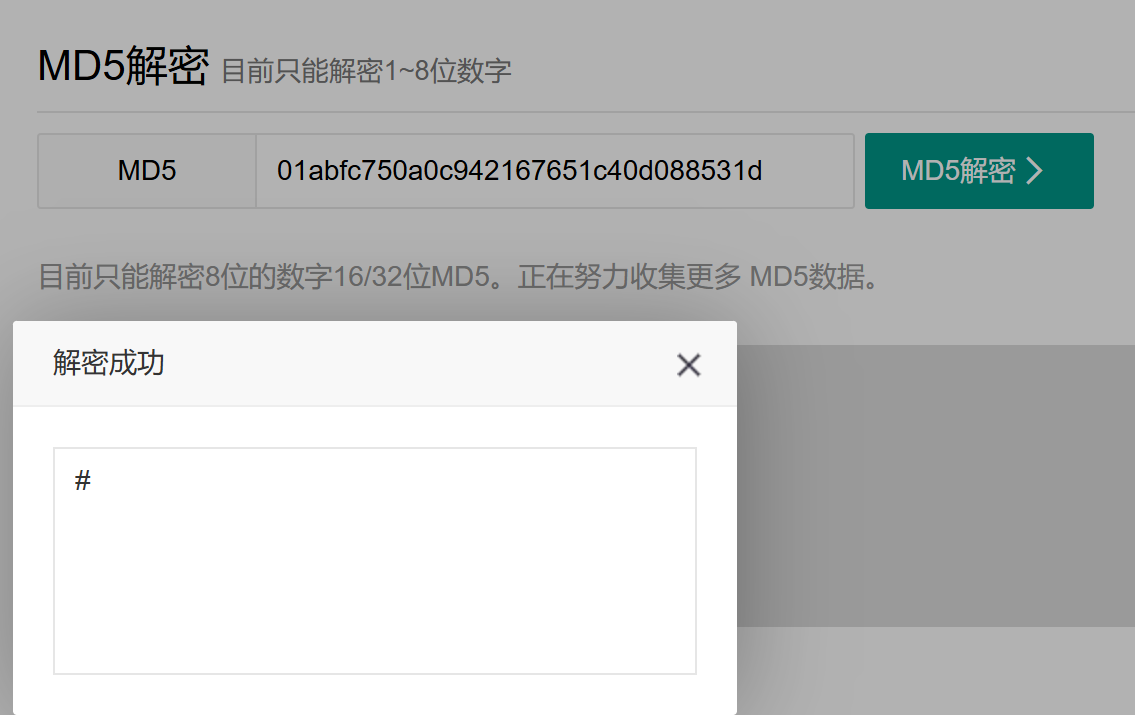
阅读.data段可获得enc[]内容，输入前给出了一个提示puts("func(?)=\"01abfc750a0c942167651c40d088531d\"?");

对32位数字做md5解密，得到字符’#’，猜测这是输入字符串的开头。

因此可以写出exp

enc = [0xF3, 0x2E, 0x18, 0x36, 0xE1, 0x4C, 0x22, 0xD1, 0xF9, 0x8C, 0x40, 0x76, 0xF4, 0x0E, 0x00, 0x05, 0xA3, 0x90, 0x0E, 0xA5]

input = '#'

k = len(input)

for j in range(len(enc)):
    input += chr(((enc[j] ^ ((ord(input[j]) ^ 18) * 3 + 2)) - (ord(input[j]) % 7)) & 0xFF)

print(input)