[Crypto]群理论

一、代数运算

定义12.1

设 $M$ 是一个非空集合，如果存在一个对应规则 $f$，使得对 $M$ 中任意两个元素 $a$ 和 $b$ ，在 $M$ 中都有唯一确定的元素 $c$ 与它们对应，则称 $f$ 为 $M$ 上的一个代数运算(二元运算)，记作 $c=f(a,b)$ 或简记为$c=a·b$ .（封闭性）

判断集合 $M$ 上运算的封闭性

如果封闭：
- 证明对于所有 $a, b \in M$，运算结果 $a \cdot b \in M$。
如果不封闭：
- 找到特定的元素 $a, b \in M$，使得 $a \cdot b \notin M$。

常见基本代数运算

自然数集 $N$ 上的加法、乘法运算；
整数集 $Z$ 上的加法、减法与乘法运算；
有理数集 $Q$ 上的加法、减法和乘法运算；
非零有理数集 $Q^*$ 上的乘法与除法运算；
有理数、实数上全体 $n$ 阶方阵的加法与乘法运算；
有理数、实数上全体 $n$ 阶可逆方阵的乘法运算。

定义 12.2

设 $n$ 是大于 1 的任意正整数，集合 $Z_n$ 定义为：

$$ Z_n = {0, 1, 2, \ldots, n-1} $$

集合 $Z_n$ 中如下两种运算为代数运算：

模 $n$ 的加法：$a \oplus b = a + b \mod n$
模 $n$ 的乘法：$a \otimes b = a \times b \mod n$

二、群的定义

定义 12.3

设 $G$ 是一个非空集合，$\cdot$ 是 $G$ 上的一个代数运算（即满足封闭性），如果该运算满足以下三条性质：

结合律：对于所有 $a, b, c \in G$，有 $(a \cdot b) \cdot c = a \cdot (b \cdot c)$。
有单位元：存在 $e \in G$，对于所有 $a \in G$，有 $e \cdot a = a$。
有逆元：对于所有 $a \in G$，存在 $a’ \in G$，使得 $a \cdot a’ = a’ \cdot a = e$。

则称 $(G , \cdot)$ 为一个群（Group）。

注：在群只有一个运算时可简称 $G$ 为一个群。

常见群的例子

例1：整数加群，有理数加群，实数加群。
例2：非零有理数关于乘法构成群，非零实数关于乘法构成群。
例3：整数、有理数、实数上n阶方阵加群。有理数、实数上n阶可逆方阵乘法群。

例 7

设 $n$ 是大于 1 的任意正整数，剩余类集 $Z_n = {0, 1, 2, \ldots, n-1}$。

关于如下模 $n$ 的加法运算为群：

$$a \oplus b = a + b \mod n$$

思考一下：关于如下模 $n$ 的乘法运算为群吗？

$$a \otimes b = a \times b \mod n$$

$Z_n$ 关于模 $n$ 的乘法不是群，因为元素 0 没有逆元。
$Z_n \setminus {0}$ 关于模 $n$ 的乘法是否是群？
$Z_n \setminus {0}$ 关于模 $n$ 的乘法只有当 $n$ 为素数时才是群，一般情况下 $n$ 的因子没有逆元。

例 8

设 $n$ 是大于 1 的任意正整数，集合 $Z_n^* = { a | a \in Z_n, (a, n) = 1 }$。

关于模 $n$ 的乘法运算为群：

$$ a \otimes b = a \times b \mod n $$

12.1.5 群的阶

由于群里结合律是满足的，把元素 $g$ 的 $m$ 次运算记为 $g^m$，称为 $g$ 的 $m$ 次幂。
$$ g^m = g \cdot g \cdots g \quad \text{(共 } m \text{ 个 } g) $$
当群运算用加法表示时，
$$ mg = m \cdot g = g + g + \cdots + g \quad \text{(共 } m \text{ 个 } g) $$

定义 12.4

如果一个群 $G$ 中元素的个数是无限多个，则称 $G$ 是无限群；如果 $G$ 中的元素个数是有限多个，则称 $G$ 是有限群， $G$ 中元素的个数称为群的阶（Order），记为 $|G|$。

群可分为：有限群与无限群
- 模 $n$ 的剩余类加法群、乘法群， $n$ 次对称群等为有限群；
- 一般线性群、特殊线性群、整数加群等为无限群。

定义 12.5

群 $G$ 中的元素 $a$ 如果存在正整数 $n$ 使得 $a^n = e$，则称 $a$ 为有限阶元，否则称为无限阶元。当 $a$ 为有限阶元时，称使得 $a^n = e$ 的最小正整数为元素 $a$ 的阶，记为 $|a|$。

群 $\left(\mathbb{Z}_6, \oplus\right)$ 阶为6，元素2的阶为3。

在群 $\left(\mathbb{Z}_{11}^*, \otimes\right)$ 中，求出2的阶为10。

定理 12.6

对于有限群 $G$，元素 $a$ 属于群 $G$：

对于整数 $n$，则 $a^n = e \Leftrightarrow |a| \mid n$。
$\left|a^i\right| = \frac{|a|}{(|a|, i)}$。
$a$ 的阶数整除群 $G$ 的阶数。

阶为素数 $p$ 的群除了单位元外其他元素阶都为 $p$。
若有限群 $G$ 中元素 $a$ 的阶等于 $G$ 的阶，则 $a$ 称为 $G$ 的生成元（即 $a$ 的幂次遍历所有元素），这种可由一个元素幂次生成的群称为循环群。

推论 12.6：素数阶群 $G$ 必须是循环群，且除单位元外每一个元素 $a$ 都是生成元。

定义 12.7

设 $G$ 是一个群，$H$ 是 $G$ 的非空子集，如果 $H$ 关于群 $G$ 的运算也构成一个群，那么称 $H$ 是 $G$ 的子群（subgroup），记为 $H \leq G$。

对于有限群 $G$ 中元素 $b$，如果 $b$ 的阶为 $k$，则 $${b, b^2, \ldots, b^k}$$ 为 $G$ 的子群。

子群的阶必然整除群的阶（拉格朗日定理）。

一类特殊群：格

$$\Lambda = { z_1 b_1 + z_2 b_2 \mid z_1, z_2 \in \mathbb{Z} }$$关于加法向量构成群

由于系数是整数，不能组成一个连续的线性空间了。向量只会构成一个密布的、网格状的离散集合。其中每一个点都代表一个可以基向量的线性组合表示的一个独特向量。

这个特殊的群称为格。

设$n$ 是大于 1 的正整数，实数 $\mathbb{R}$ 上的 $n$ 个 $n$ 维的线性无关向量
$${\vec{a}_1, \vec{a}_2, \ldots, \vec{a}_n \mid \vec{a}_i \in \mathbb{R}^n}$$
整系数线性组合全体 ( L )
$$L = {\sum_{1 \leq i \leq n} b_i \vec{a}_i \mid b = \left(b_1, b_2, \ldots, b_n\right) \in \mathbb{Z}^n}$$
关于向量加法构成群。

例如：

$$b_1 = (0.7, 0.4), b_2 = (0.8, 0.5)$$

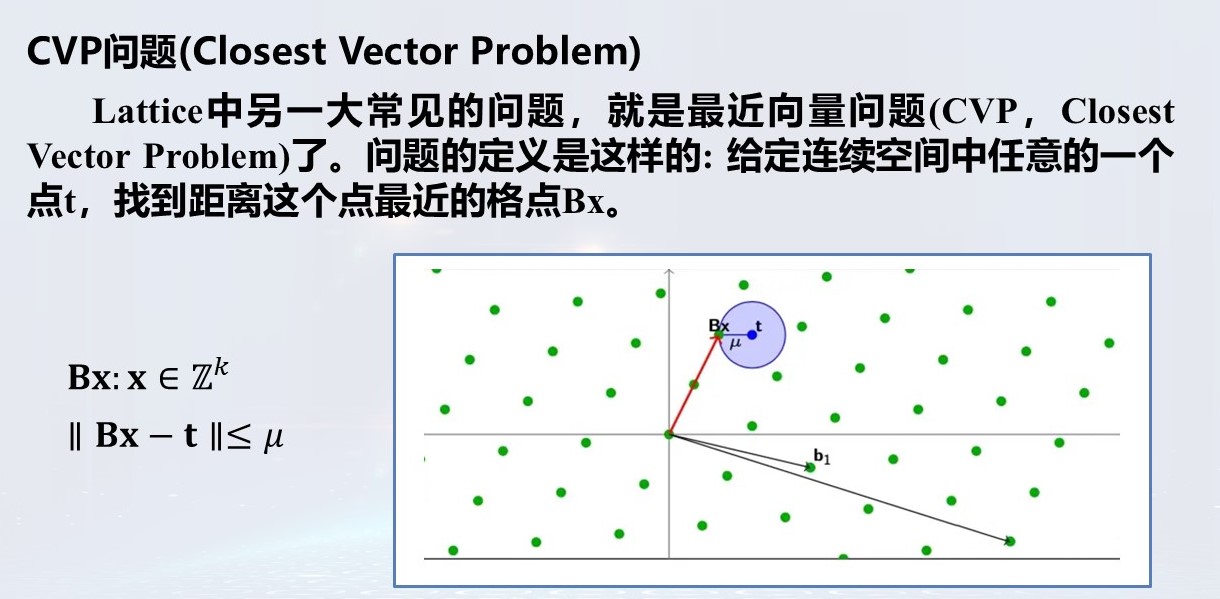
格中最短非零向量？（最短向量问题SVP）
$c = (2.6, 3.1)$ 是否属于格？

如果不是，格中距离最近向量是？（最近向量问题CVP）

$$ \binom{0.7}{0.4} \times 1 + \binom{0.8}{0.5} \times 2 = \binom{2.5}{3.1} $$

即

$$ \left(\begin{array}{ll} 0.7 & 0.8 \\ 0.4 & 0.5 \end{array}\right) \left(\begin{array}{l} x_1 \\ x_2 \end{array}\right)= \left(\begin{array}{l} 2.5 \\ 3.1 \end{array}\right) $$

利用高斯消除法容易求得 $x_1 = -41, x_2 = 39$。

如果改成

$$ \left(\begin{array}{ll} 0.7 & 0.8 \\ 0.4 & 0.5 \end{array}\right) \left(\begin{array}{l} x_1 \\ x_2 \end{array}\right)= \left(\begin{array}{l} 2.6 \\ 3.1 \end{array}\right) $$

高斯消除法得 $x_1 = -\frac{118}{3}, x_2 = \frac{113}{3}$。

求整数解

$$ \left(\begin{array}{ll} 0.7 & 0.8 \\ 0.4 & 0.5 \end{array}\right) \left(\begin{array}{l} x_1 \\ x_2 \end{array}\right) \approx \binom{2.6}{3.1} \quad $$

（带学习误差问题LWE）

enter image description here